Раскраска графа алгоритм
![Как раскрасить вершины графа / Хабр [В работе] Конспект лекции по раскраскам](https://upload.wikimedia.org/wikipedia/commons/thumb/9/90/Petersen_graph_3-coloring.svg/220px-Petersen_graph_3-coloring.svg.png)
Кто сталкивался с программной реализацией переборного алгоритма для раскраски графа?
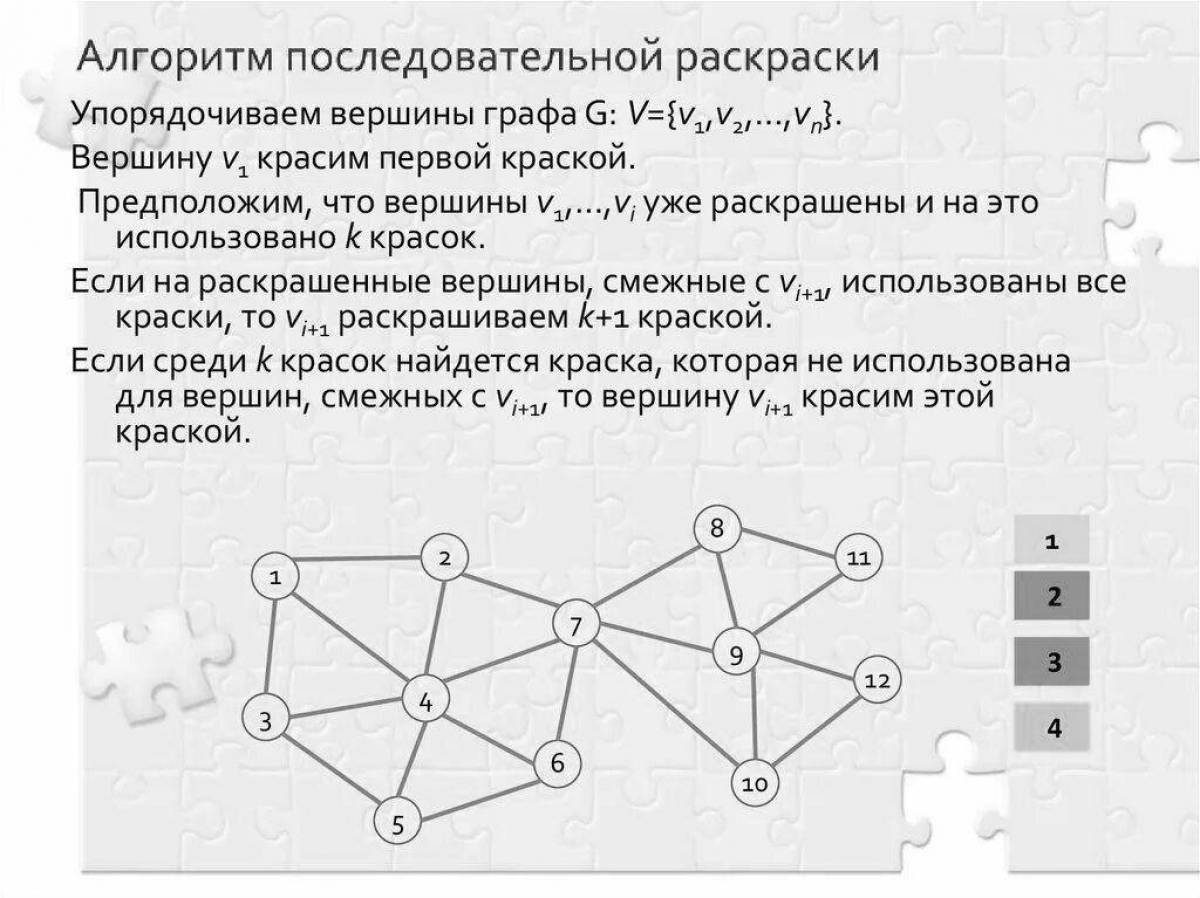
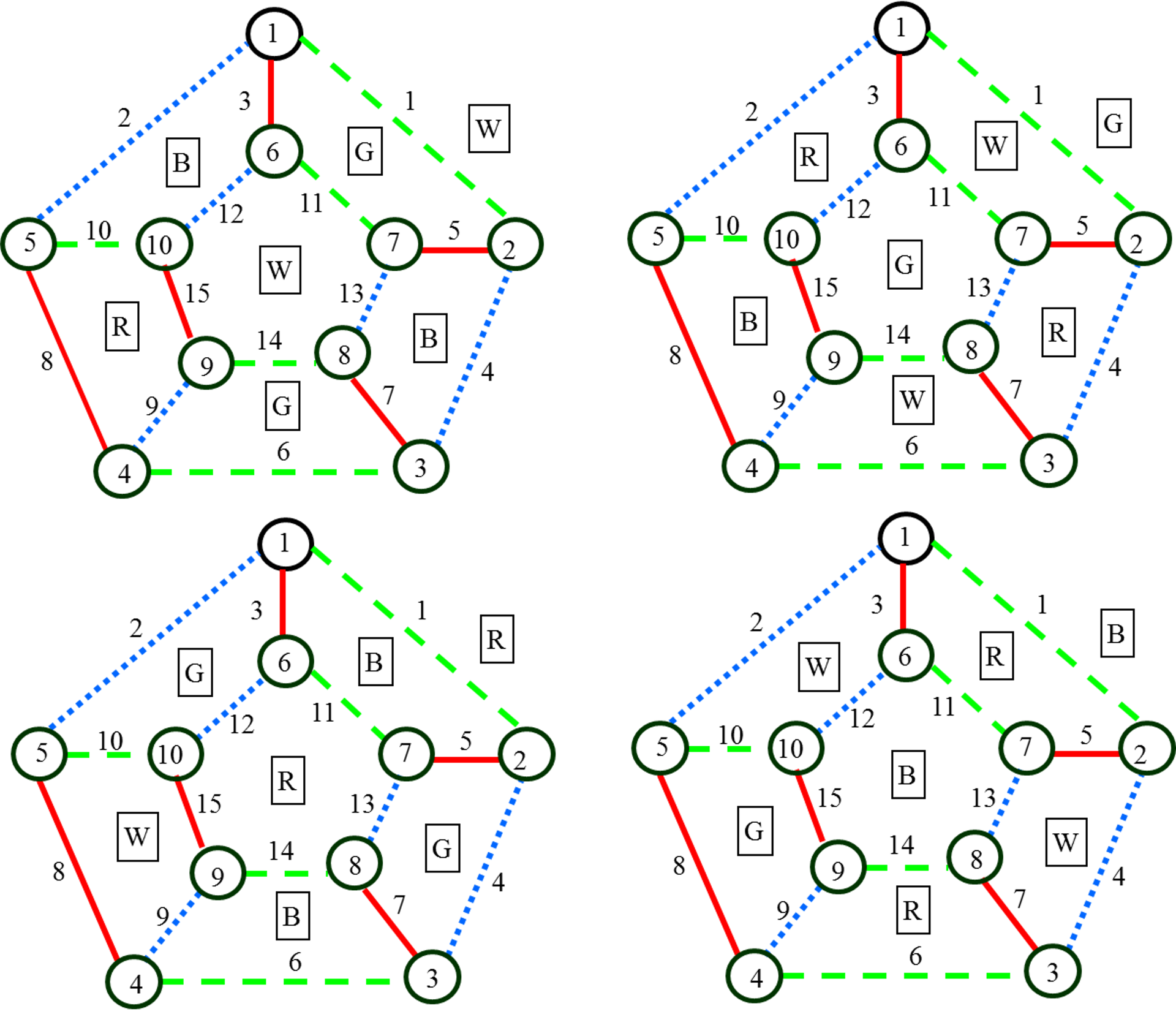
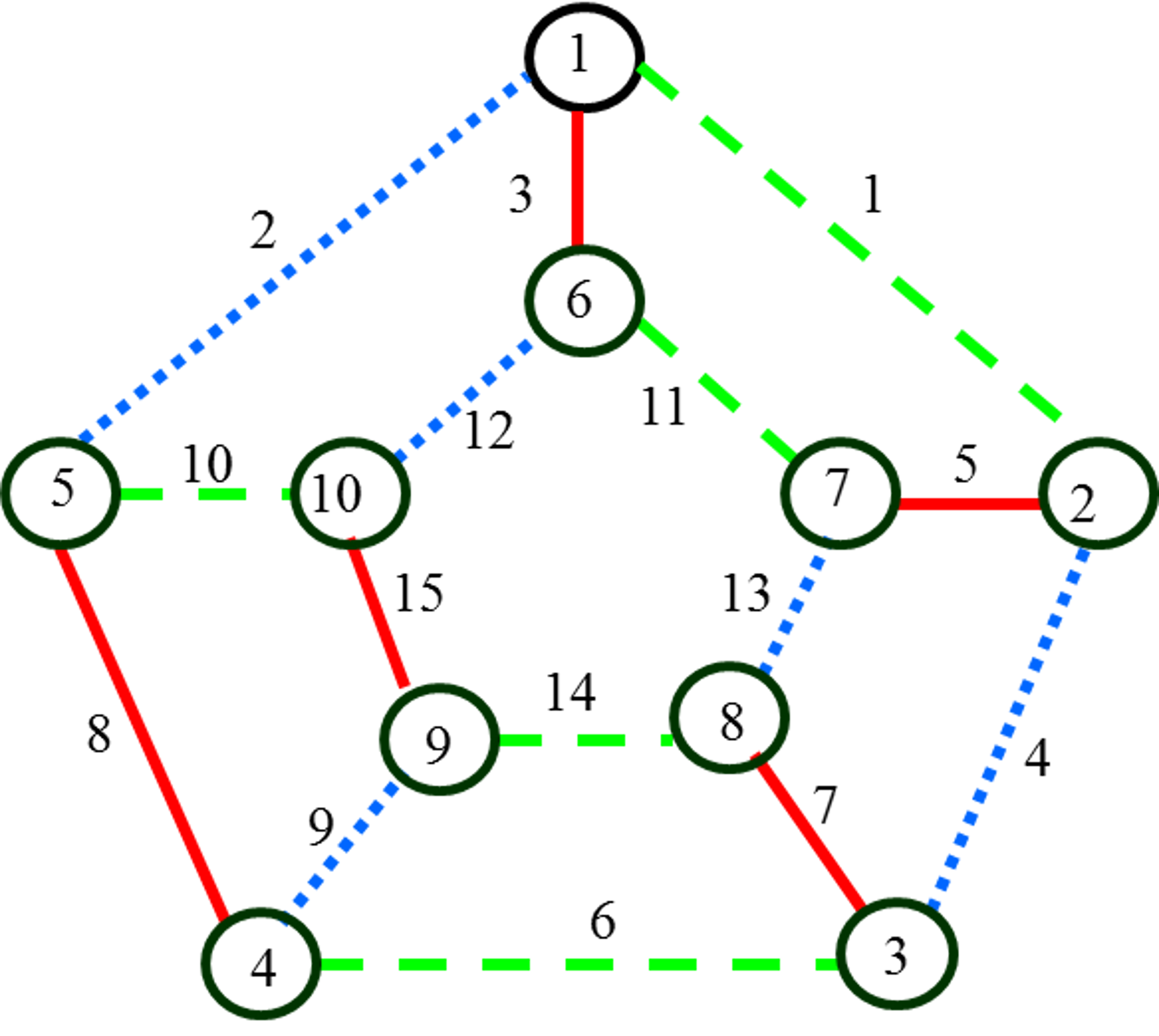
На этом шаге мы рассмотрим алгоритмы закраски графа. Задачи определения хроматического числа и построения минимальной раскраски произвольного графа являются очень сложными. С одной стороны, не известны алгоритмы их решения, сложность которых есть некоторая фиксированная степень от длины записи условий задачи так называемые полиномиальные алгоритмы. С другой стороны, нигде явно не выражены те потери, которые мы несем от отсутствия таких алгоритмов [1, с.






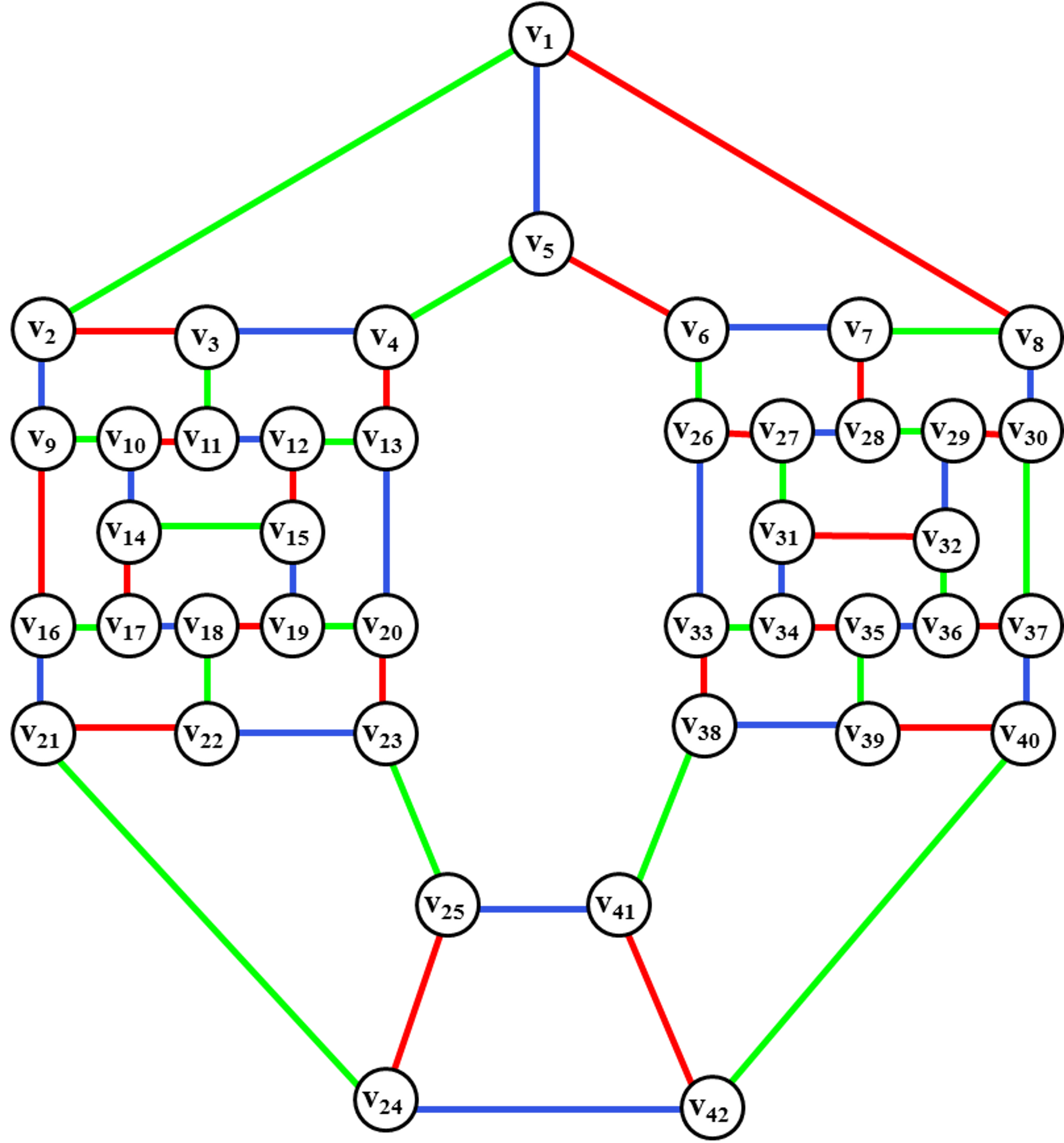
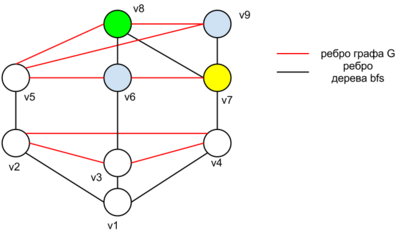
Когда говорят о раскраске графов, почти всегда подразумевают под этим раскраску их вершин, то есть присвоение цветовых меток вершинам графа так, чтобы любые две вершины, имеющие общее ребро, имели разные цвета. Так как графы, в которых есть петли, не могут быть раскрашены таким образом, они не являются предметом обсуждения. Полный граф - такой граф, у которого есть путь из каждой вершины в каждую. Очевидно, что хроматическое число полного графа совпадает с количеством вершин.


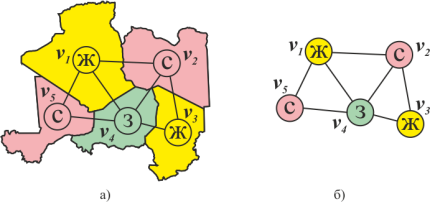

![[В работе] Конспект лекции по раскраскам [lihman.ru]](https://studfile.net/html/66814/245/html_aMzjD3utYx.FKmY/htmlconvd-Ove4hx_html_e9eaf7ee46650d5e.png)

Алгоритм раскраски графа позволяет находить точное или приближенное значение хроматического числа произвольного графа и соответствующую этому значению раскраску вершин. Граф G называют r-хроматическим, если его вершины могут быть раскрашены с использованием r цветов красок так, что не найдется двух смежных вершин одного цвета. Наименьшее число r, такое, что граф G является r-хроматическим, называется хроматическим числом графа G.